DDE-Biftool demo Mackey-Glass Equation

The Mackey-Glass equation is given by

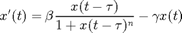
Parameters are (in this order) beta, n, tau (gamma is not part of parameter vector).

(c) DDE-BIFTOOL v. 3.1.1(73), 31/12/2014

Contents

load DDE-Biftool into path

clear
close all
addpath('../../ddebiftool',...
    '../../ddebiftool_extra_psol',...
    '../../ddebiftool_extra_nmfm',...
    '../../ddebiftool_utilities');

Enable vectorization

(disable for speed comparison)

x_vectorize=true;

Set user-defined functions

using gamma as constant and (beta,|n|,|tau|) as parameters

gamma=1.0;
beta_ind=1;
n_ind=2;
tau_ind=3;
if x_vectorize
    f=@(x,xtau,beta,n)beta*xtau./(1+xtau.^n)-gamma*x;
    funcs=set_funcs(...
        'sys_rhs',@(xx,p)f(xx(1,1,:),xx(1,2,:),p(1),p(2)),...
        'sys_tau',@()tau_ind,...
        'x_vectorized',true);
else
    f=@(x,xtau,beta,n)beta*xtau/(1+xtau^n)-gamma*x; %#ok<UNRCH>
    funcs=set_funcs(...
        'sys_rhs',@(xx,p)f(xx(1,1,:),xx(1,2,:),p(1),p(2)),...
        'sys_tau',@()tau_ind);
end

Initial parameters and state

beta0=2;
n0=10;
tau0=0;
x0=(beta0-1)^(1/n0);

Initialization of branch of non-trivial equilibria

contpar=tau_ind;
nontriv_eqs=SetupStst(funcs,'x',x0,'parameter',[beta0,n0,tau0],'step',0.1,...
    'contpar',contpar,'max_step',[contpar,0.3],'max_bound',[contpar,10]);

Compute and find stability of non-trivial equilibria

disp('Trivial equilibria');
figure(1);clf
nontriv_eqs=br_contn(funcs,nontriv_eqs,3);
nontriv_eqs=br_stabl(funcs,nontriv_eqs,0,1);
nunst_eqs=GetStability(nontriv_eqs);
ind_hopf=find(nunst_eqs<2,1,'last');
fprintf('Hopf bifurcation near point %d\n',ind_hopf);

Trivial equilibria
Hopf bifurcation near point 4

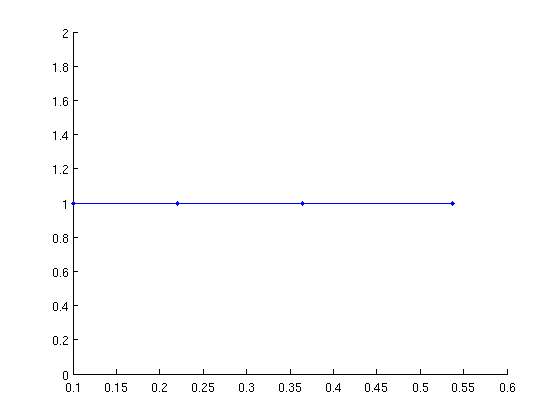
Continue Hopf bifurcation in two parameters

[hbranch,suc]=SetupHopf(funcs,nontriv_eqs,ind_hopf,...
    'contpar',[beta_ind,tau_ind],'dir',beta_ind,'step',1e-3);
figure(2);clf
hbranch=br_contn(funcs,hbranch,30);
hbranch=br_rvers(hbranch);
hbranch=br_contn(funcs,hbranch,30);

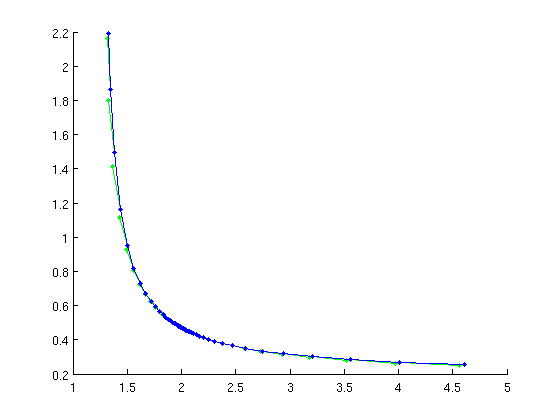
Compute L1 coefficient

to find if Hopf bifurcation is supercritical (L1<0) or subcritical (L1>0)

[L1,L1low]=HopfLyapunovCoefficients(funcs,hbranch);
fprintf('maximal L1 coefficient along Hopf branch: %g\n',max(L1));
fprintf('max of error estimate for L1 coefficient: %g\n',norm(L1-L1low,'inf'));

maximal L1 coefficient along Hopf branch: -4.22512
max of error estimate for L1 coefficient: 3.24906e-07

Branch off at Hopf bifurcation

disp('Branch off at Hopf bifurcation');
fprintf('Initial correction of periodic orbits at Hopf:\n');
[per_orb,suc]=SetupPsol(funcs,nontriv_eqs,ind_hopf,...
    'print_residual_info',1,'intervals',20,'degree',4,...
    'max_bound',[contpar,20],'max_step',[contpar,0.5]);
if ~suc
    error('MackeyGlassDemo:fail',...
        'MackeyGlassDemo: initialization of periodic orbit failed');
end
figure(1);
hold on
per_orb=br_contn(funcs,per_orb,60);
per_orb=br_stabl(funcs,per_orb,0,1);
nunst_per=GetStability(per_orb,'exclude_trivial',true);

Branch off at Hopf bifurcation
Initial correction of periodic orbits at Hopf:
it=1, res=0.678113
it=2, res=0.254197
it=3, res=0.00767615
it=4, res=4.3608e-05
it=5, res=2.39552e-10
it=1, res=0.000474015
it=2, res=2.52388e-07
it=3, res=3.16761e-13
it=1, res=2.21451e-07
it=2, res=5.91749e-14
it=1, res=0.00153112
it=2, res=1.62608e-05
it=3, res=4.24821e-08
it=4, res=1.62731e-12
it=1, res=0.00229308
it=2, res=6.5338e-05
it=3, res=4.58407e-07
it=4, res=1.33502e-11
...

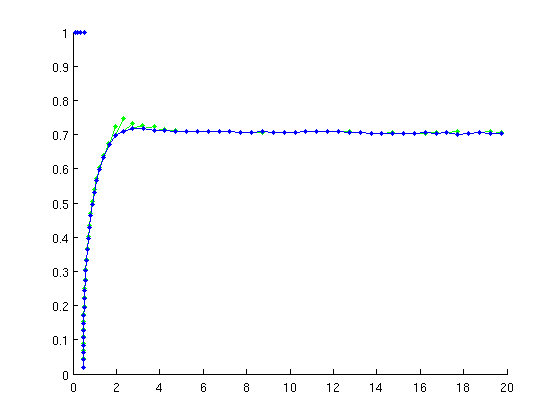
Find period doubling bifurcations in two parameters

ind_pd=find(diff(nunst_per)==1);
[pdfuncs,pdbranch1,suc]=SetupPeriodDoubling(funcs,per_orb,ind_pd(1),...
    'contpar',[beta_ind,tau_ind],'dir',beta_ind,'step',1e-3);
if ~suc
    error('MackeyGlassDemo:fail',...
        'MackeyGlassDemo: initialization of period doubling failed');
end
figure(2);
pdbranch1=br_contn(pdfuncs,pdbranch1,30);
pdbranch=br_rvers(pdbranch1);
pdbranch=br_contn(pdfuncs,pdbranch,30);

it=1, res=0.788214
it=2, res=0.0916883
it=3, res=0.00253072
it=4, res=1.56425e-07
it=5, res=3.57514e-11
it=1, res=0.0112006
it=2, res=1.16378e-08
it=3, res=2.78844e-11
it=1, res=0.0069642
it=2, res=8.98603e-06
it=3, res=1.77941e-10
it=1, res=0.00537865
it=2, res=3.24797e-09
it=1, res=0.00646205
it=2, res=8.17251e-09
it=1, res=4.45395e-05
it=2, res=1.71072e-09
it=1, res=0.00265392
it=2, res=2.07429e-09
it=1, res=0.00316854
...

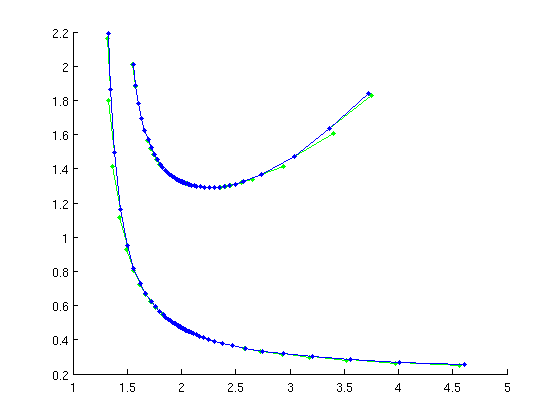
Check Floquet multipliers

(note that Floquet multipliers are often unreliable)

pd1sols=pdfuncs.get_comp(pdbranch.point,'solution');
[nunst_pd,floqpd1,triv_defect,pd1sols]=GetStability(pd1sols,...
    'exclude_trivial',true,'funcs',funcs); %#ok<ASGLU>
fprintf('max defect of Floquet multiplier at -1: %g\n',max(abs(floqpd1+1)));

max defect of Floquet multiplier at -1: 1.12158e-05

Branch off at period doubling

(Solutions at far end get inaccurate.)

[per2,suc]=DoublePsol(funcs,per_orb,ind_pd(1));
if ~suc
    error('MackeyGlassDemo:fail',...
        'MackeyGlassDemo: branching off at period doubling failed');
end
figure(1);
per2=br_contn(funcs,per2,60);
per2=br_stabl(funcs,per2,0,1);
[nunst_per2,dom,triv_defect]=GetStability(per2,'exclude_trivial',true);
fprintf('max defect of Floquet multiplier at 1: %g\n',max(triv_defect));

it=1, res=0.0121409
it=2, res=0.0273993
it=3, res=0.000295009
it=4, res=2.36294e-08
it=5, res=2.4869e-13
it=1, res=0.00152497
it=2, res=8.5076e-09
it=1, res=0.0239432
it=2, res=0.027895
it=3, res=0.000300141
it=4, res=2.43515e-08
it=5, res=2.82441e-13
it=1, res=0.00178604
it=2, res=6.37172e-09
it=1, res=0.00221106
it=2, res=6.75198e-05
it=3, res=2.11874e-07
it=4, res=5.19771e-11
it=1, res=0.00135625
it=2, res=3.22848e-05
...

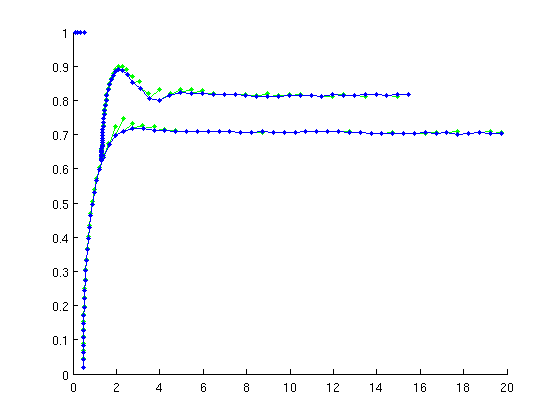
Continue period doublings in two parameters for secondary PD

ind_pd2=find(diff(nunst_per2)==1);
[pd2funcs,pdbranch2,suc]=SetupPeriodDoubling(funcs,per2,ind_pd2(1),...
    'contpar',[beta_ind,tau_ind],'dir',beta_ind,'step',1e-3);
if ~suc
    error('MackeyGlassDemo:fail',...
        'MackeyGlassDemo: initialization of 2nd period doubling failed');
end
figure(2);
pdbranch2=br_contn(pdfuncs,pdbranch2,30);
pdbranch2=br_rvers(pdbranch2);
pdbranch2=br_contn(pdfuncs,pdbranch2,30);

it=1, res=1.21029
it=2, res=0.0935189
it=3, res=0.000124173
it=4, res=2.56318e-09
it=1, res=0.0396517
it=2, res=3.78669e-08
it=3, res=7.95417e-11
it=1, res=0.0242439
it=2, res=3.87749e-05
it=3, res=1.19399e-09
it=1, res=0.0248964
it=2, res=7.4681e-08
it=3, res=8.08447e-11
it=1, res=0.0298027
it=2, res=1.74531e-07
it=3, res=7.02087e-11
it=1, res=0.000163317
it=2, res=1.19874e-08
it=3, res=7.5671e-11
it=1, res=0.0210909
...

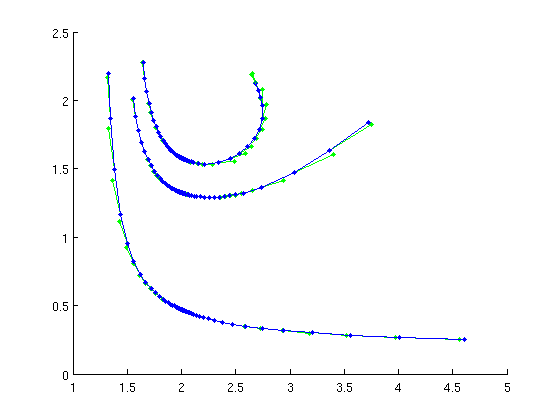
Check Floquet multipliers along period doubling bifurcation

(Note that Floquet multipliers are often unreliable.)

pd2sols=pdfuncs.get_comp(pdbranch2.point,'solution');
[nunst_pd2,floqpd2,triv_defect,pd2sols]=GetStability(pd2sols,...
    'exclude_trivial',true,'funcs',funcs);
fprintf('max defect of Floquet multiplier at -1: %g\n',max(abs(floqpd2+1)));

max defect of Floquet multiplier at -1: 6.42923e-05

Plot of period doubling bifurcation x profiles

bifsols={pd1sols,pd2sols,hbranch.point};
floqpd={floqpd1,floqpd2};
get_par=@(i,k)arrayfun(@(x)x.parameter(i),bifsols{k});
figure(3)
clf;
subplot(3,2,[1,2]);
plot(get_par(beta_ind,1),get_par(tau_ind,1),'.-',...
    get_par(beta_ind,2),get_par(tau_ind,2),'.-',...
    get_par(beta_ind,3),get_par(tau_ind,3),'.-');
legend('PD1','PD2','Hopf');
xlabel('\beta');
ylabel('\tau');
title(sprintf(['Hopf, 1st and 2nd period doubling in Mackey-Glass eqn, ',...
    ' n=%g, gamma=1'],n0));
grid on
for k=1:2
    subplot(3,2,2+k);
    hold on
    for i=1:length(bifsols{k})
        plot(bifsols{k}(i).mesh*bifsols{k}(i).period,bifsols{k}(i).profile,'-');
    end
    hold off
    box on
    grid on
    title(sprintf('PD%d: time profiles of period doubling',k));
    xlabel('t');
    ylabel('x');
    subplot(3,2,4+k);
    plot(1:length(bifsols{k}),floqpd{k}+1,'.-');
    grid on
    title(sprintf('PD%d: dist crit Floq mult from -1',k));
    ylabel('error');
    xlabel('point along branch');
end

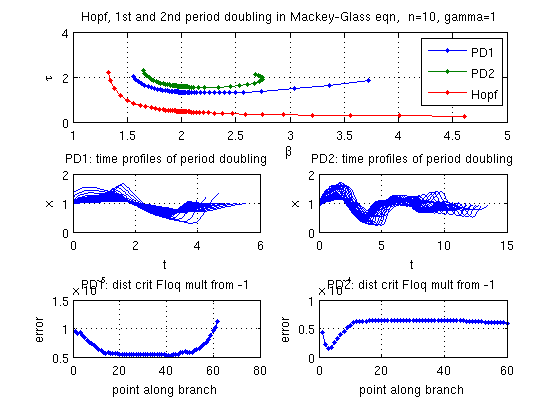
save

save('MGresults.mat');

Published with MATLAB® 7.14