Demo for state-dependent delays --- example from Humpries etal (DCDS-A 2012)

% (c) DDE-BIFTOOL v. 3.1.1(20), 11/04/2014

Humphries et al ( A. R. Humphries, O. A. DeMasi, F. M. G. Magpantay, F. Upham (2012), Dynamics of a delay differential equation with multiple state-dependent delays, Discrete and Continuous Dynamical Systems 32(8) pp. 2701-2727 http://dx.doi.org/10.3934/dcds.2012.32.2701)

consider a scalar DDE with two state-dependent delays:

$$x'(t)=-\gamma x(t)-\kappa_1 x(t-a_1-c x(t))-\kappa_2 x(t-a_2-c x(t))\mbox{.}$$

The system exhibits double Hopf bifurcations, folds of periodic orbits and torus bifurcations, which can be computed and demonstrated using DDE-Biftool.

Contents

Add path to DDE-Biftool

clear
close all
addpath('../../ddebiftool/',...
    '../../ddebiftool_extra_psol/',...
    '../../ddebiftool_utilities/');

Function definitions (right-hand side and delays)

Define the right-hand side and the state-dependent delays. We also provide their derivatives (in separate functions) to speed up execution.

Order of the parameters: p(1:2)=kappa1:2, p(3:4)=a1:2, p(5)=gamma, p(6)=c

rhs=@(x,p)-p(5)*x(1,1,:)-p(1)*x(1,2,:)-p(2)*x(1,3,:);
sys_ntau=@()2;
tau=@(nr,x,p)p(2+nr)+p(6)*x(1,1,:);
drhs=@(x,p,nx,np,v)sys_deri_humphries_etal(rhs,x,p,nx,np,v);
dtau=@(nr,x,p,nx,np)sys_dtau_humphries_etal(tau,nr,x,p,nx,np);
funcs=set_funcs('sys_rhs',rhs,'sys_ntau',sys_ntau,'sys_tau',tau,...
    'sys_deri',drhs,'sys_dtau',dtau,'x_vectorized',true);
par_ini=[0,2.3,1.3,6,4.75,1];
indkappa1=1;
indkappa2=2;

Trivial equilibrium branch

The equilibrium 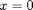$x=0$ changes its stability in Hopf bifurcations

[eqbr,suc]=SetupStst(funcs,'contpar',indkappa1,'x',0,'parameter',par_ini,...
    'max_bound',[indkappa1,12],'max_step',[indkappa1,0.1]);
if ~suc
    error('equilibrium not found');
end
clf
eqbr=br_contn(funcs,eqbr,100);
% stability
[eqnunst,dom,triv_defect,eqbr.point]=...
GetStability(eqbr,'funcs',funcs,'points',2:length(eqbr.point));

Periodic orbits branching off from 1st Hopf bifurcation

We continue the periodic orbits in parameter(1) (kappa1), and calculate their stability.

indhopf=find(eqnunst>0,1,'first');
[per,suc]=SetupPsol(funcs,eqbr,indhopf,'contpar',indkappa1,'degree',5,'intervals',30,...
    'print_residual_info',1,'radius',1e-2);
if ~suc
    error('initialization of periodic orbits failed');
end
per.parameter.max_step=[indkappa1,0.3];
per=br_contn(funcs,per,200);
disp('calculate stability')
[pernunst,dom,triv_defect,per.point]=...
    GetStability(per,'exclude_trivial',true,'funcs',funcs); %#ok<*ASGLU>
fprintf('maximum error of trivial Floquet multiplier: %g\n',max(abs(triv_defect)));

it=1, res=0.00670715
it=2, res=5.70491e-06
it=3, res=2.7812e-12
it=1, res=0.0171466
it=2, res=2.54493e-06
it=3, res=8.88453e-14
it=1, res=3.03196e-09
it=1, res=0.0462999
it=2, res=5.17741e-05
it=3, res=3.97891e-08
it=4, res=2.14688e-14
it=1, res=0.0612862
it=2, res=0.000409528
it=3, res=1.4835e-06
it=4, res=1.48815e-11
it=1, res=1.59646e-08
it=2, res=2.21728e-14
it=1, res=0.0680922
it=2, res=0.000754814
it=3, res=3.24181e-06
...

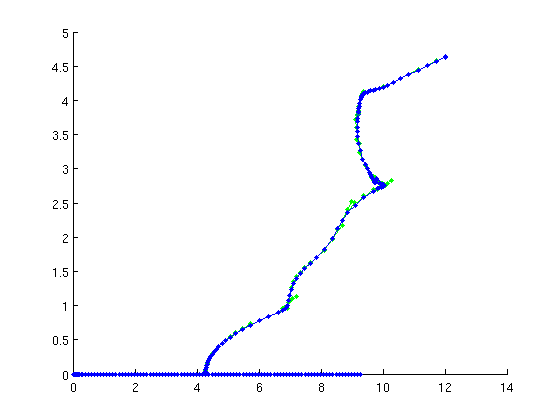
One-parameter bifurcation diagram for family of periodic orbits

Continuation parameter is 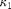$\kappa_1$.

ppars=arrayfun(@(x)x.parameter(1),per.point);
pmeshes=cell2mat(arrayfun(@(x)x.mesh(:),per.point,'uniformoutput',false));
pprofs=cell2mat(arrayfun(@(x)x.profile(1,:)',per.point,'uniformoutput',false));
clf
clrs=colormap('lines');
pernunst_cases=unique(pernunst);
amp=max(pprofs)-min(pprofs);
hold on
lstr={};
for i=1:length(pernunst_cases);
    sel=pernunst==pernunst_cases(i);
    plot(ppars(sel),amp(sel),'o','color',clrs(i,:));
    lstr={lstr{:},sprintf('#unst=%d',pernunst_cases(i))}; %#ok<CCAT>
end
hold off
grid on
xlabel('\kappa_1');
ylabel('amplitude');
legend(lstr,'location','southeast');
grid on

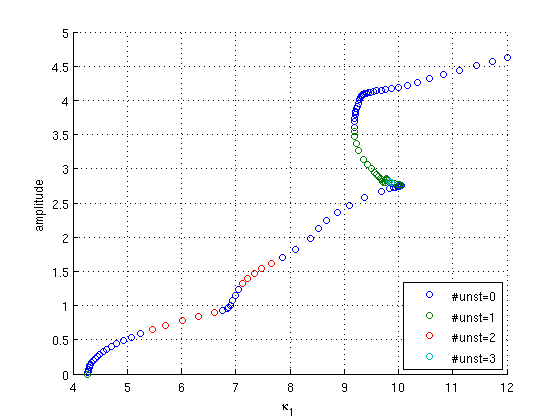
save('humphries1dbif.mat');

Hopf bifurcation in two parameters

Continuation parameters are 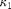$\kappa_1$ and $\kappa_2$.

figure(2);clf
[hbranch1,suc]=SetupHopf(funcs,eqbr,indhopf,...
    'contpar',[indkappa1,2],'dir',indkappa1,'step',0.1,...
    'max_bound',[indkappa1,12; indkappa2,10],...
    'min_bound',[indkappa1,0; indkappa2,0],...
    'max_step',[indkappa1,0.1; indkappa2,0.1]);
if ~suc
    error('Hopf initialization failed');
end
clf
hbranch1=br_contn(funcs,hbranch1,100);
hbranch1=br_rvers(hbranch1);
hbranch1=br_contn(funcs,hbranch1,100);
hpars=cell2mat(arrayfun(@(x)x.parameter(1:2)',hbranch1.point,'uniformoutput',false));

BR_CONTN warning: boundary hit.
BR_CONTN warning: boundary hit.

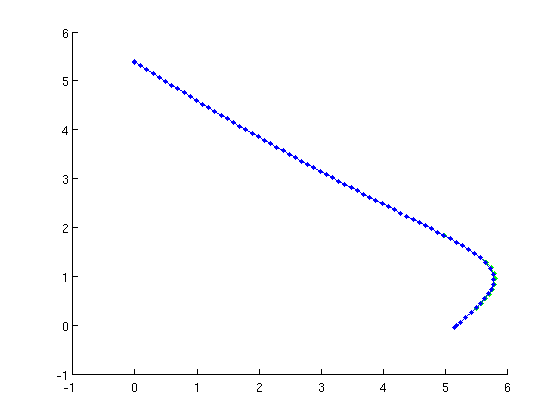
Fold of periodic orbits

Continuation parameters are 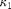$\kappa_1$ and $\kappa_2$. We remove stepsize restrictions for parameters, increase the maximum number of Newton iterations. The stability along the fold may indicate codimensions. However, increasing triv_defect indicates increasing errors in Floquet multiplier computations.

pf_ind0=find(diff(pernunst)==1,1,'first');
per.method.point.print_residual_info=1;
per.parameter.max_step=[];
per.method.point.newton_max_iterations=8;
[pfuncs,pbr,suc]=SetupPOfold(funcs,per,pf_ind0,'contpar',[indkappa1,indkappa2],...
    'dir',indkappa2,'step',-0.01);
if ~suc
    error('initialization of fold of periodic orbits failed');
end

it=1, res=3.08797
it=2, res=204.739
it=3, res=13.8964
it=4, res=0.10911
it=5, res=2.02177e-06
it=6, res=1.60907e-11
it=1, res=6.90913
it=2, res=0.109275
it=3, res=3.54579e-06
it=4, res=1.68807e-11
it=1, res=5.03447
it=2, res=2.5498
it=3, res=0.00157249
it=4, res=2.57639e-09
it=1, res=3.53685
it=2, res=0.137775
it=3, res=1.54648e-06
it=4, res=1.80291e-11

figure(2);
pbr=br_contn(pfuncs,pbr,220);
pbr=br_rvers(pbr);
pbr=br_contn(pfuncs,pbr,60);
pforbits=pfuncs.get_comp(pbr.point,'solution');
[pfstab,dom,triv_defect,pforbitstab]=GetStability(pforbits,'exclude_trivial',true,...
    'locate_trivial',@(p)[1,1],'funcs',funcs);
pfpars=cell2mat(arrayfun(@(x)x.parameter(1:2)',pbr.point,'uniformoutput',false));
pfmeshes=cell2mat(arrayfun(@(x)x.mesh(:),pbr.point,'uniformoutput',false));
pfprofs=cell2mat(arrayfun(@(x)x.profile(1,:)',pbr.point,'uniformoutput',false));
pf_amp=max(pfprofs)-min(pfprofs);
save('humphries_pofold.mat');

it=1, res=4.67569
it=2, res=0.237738
it=3, res=8.1448e-06
it=4, res=1.57667e-11
it=1, res=8.65029
it=2, res=0.0106624
it=3, res=1.00242e-07
it=4, res=1.87544e-11
it=1, res=4.97287
it=2, res=0.0112096
it=3, res=8.28609e-09
it=1, res=15.6081
it=2, res=0.0563395
it=3, res=3.99449e-06
it=4, res=1.63558e-11
it=1, res=19.9819
it=2, res=0.0517287
it=3, res=1.94464e-06
it=4, res=1.68261e-11
it=1, res=25.2063
...

Torus bifurcation continuation

Continuation parameters are 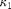$\kappa_1$ and $\kappa_2$.

tr_ind0=find(diff(pernunst)==2,1,'first');
[trfuncs,trbr,suc]=SetupTorusBifurcation(funcs,per,tr_ind0,...
    'contpar',[indkappa1,indkappa2],'dir',indkappa2,'step',-0.01);
if ~suc
    error('initialization of torus bifurcation failed');
end

it=1, res=1.86284
it=2, res=0.117783
it=3, res=9.31292e-05
it=4, res=7.96251e-09
it=1, res=0.000106411
it=2, res=4.74679e-11
it=1, res=0.644099
it=2, res=0.0584185
it=3, res=2.90345e-05
it=4, res=2.84816e-08
it=5, res=4.46003e-11
it=1, res=8.53383e-05
it=2, res=8.48063e-11

figure(2);
trbr=br_contn(trfuncs,trbr,80);
trbr=br_rvers(trbr);
trbr=br_contn(trfuncs,trbr,40);

it=1, res=0.168894
it=2, res=8.17217e-05
it=3, res=4.22518e-09
it=1, res=0.255921
it=2, res=0.000166909
it=3, res=1.25776e-08
it=4, res=7.84441e-13
it=1, res=0.000127848
it=2, res=6.26392e-11
it=1, res=0.391092
it=2, res=0.000343442
it=3, res=3.57833e-08
it=4, res=1.33626e-12
it=1, res=0.600864
it=2, res=0.000717279
it=3, res=9.8836e-08
it=4, res=3.52034e-12
it=1, res=0.92931
it=2, res=0.00160062
it=3, res=2.69597e-07
...

Stability of periodic orbits along torus bifurcation

The code below demonstrates how one can use GetStability and its optional argument 'locate_trivial' to exclude the known critical Floquet multipliers from the stability consideration. Thus, the stability changes along the torus bifurcation help detect codimension-two bifurcations.

trorbits=trfuncs.get_comp(trbr.point,'solution');
trrot=trfuncs.get_comp(trbr.point,'omega');
trorbits=arrayfun(@(x,y)setfield(x,'parameter',[x.parameter,y]),trorbits,trrot);
trivial_floqs=@(p)[1,exp(1i*p.parameter(end)*pi),exp(-1i*p.parameter(end)*pi)];
[trstab,dom,triv_defect,trorbitstab]=GetStability(trorbits,'exclude_trivial',true,...
    'locate_trivial',trivial_floqs,'funcs',funcs);

Extract parameters, meshes and profiles of orbits at torus bifurcation

trpars=cell2mat(arrayfun(@(x)x.parameter(1:2)',trbr.point,'uniformoutput',false));
trmeshes=cell2mat(arrayfun(@(x)x.mesh(:),trbr.point,'uniformoutput',false));
trprofs=cell2mat(arrayfun(@(x)x.profile(1,:)',trbr.point,'uniformoutput',false));
tr_amp=max(trprofs)-min(trprofs);
trmu=cell2mat(arrayfun(@(x)x.stability.mu(1:10),trorbitstab,'uniformoutput',false));

plot profiles of orbits at torus bifurcation

figure(3);clf
plot(trmeshes,trprofs);
grid on
xlabel('t/T');
ylabel('x');

bifucation diagram

figure(2);clf
hold on
unstabsel=trstab>0;
lw={'linewidth',2};
plot(trpars(1,unstabsel),trpars(2,unstabsel),'ro','markersize',4,'markerfacecolor','r',lw{:});
plot(hpars(1,:),hpars(2,:),'k-',...
    trpars(1,:),trpars(2,:),'r-',...
    pfpars(1,:),pfpars(2,:),'b-',lw{:});
set(gca,'xlim',[0,12],'ylim',[0,4]);
grid on
xlabel('\kappa_1');
ylabel('\kappa_2');
legend({'torus bif (unstab)','Hopf','torus bif','fold'},...
    'location','southwest');

save('humphries_2dbif.mat');


Published with MATLAB® 7.14