DDE-BIFTOOL Minimal demo for continuation of local bifurcations of periodic orbits

(c) DDE-BIFTOOL v. 3.1.1(86), 07/01/2015

This demo illustrates how to track local bifurcations of periodic orbits in DDEs with contant delay, using the extension ddebiftool_extra_psol and the auxiliary functions in ddebiftool_utilities. The example is the Duffing oscillator with delayed feedback discussed in the large-delay limit by Yanchuk & Perlikowski in (PRE79,0462211,2009):

$$x''(t)+d*x'(t)+a*x(t)+x^3+b*[x(t)-x(t-\tau)]=0$$

The parameters are 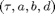$(\tau,a,b,d)$ (used in this order in the parameter vector).

Contents

Define path and system

First we load the folder of DDE-Biftool and its extensions into the Matlab path, and define the right-hand side and the delays. We create the structure containing the user-defined functions using set_funcs. We define the right-hand side such that it ca nbe called in vectorized form.

clear
close all
addpath('../../ddebiftool',...
    '../../ddebiftool_extra_psol',...
    '../../ddebiftool_extra_nmfm/',...
    '../../ddebiftool_utilities');
indtau=1;
indb=3;
funcs=set_funcs(...
    'sys_rhs',@(x,p)[...
    x(2,1,:);...
    -p(4)*x(2,1,:)-p(2)*x(1,1,:)-x(1,1,:).^3-p(indb)*(x(1,1,:)-x(1,2,:))],...
    'sys_tau',@()indtau,'x_vectorized',true);

First step: continuation of equilibria, Hopf bifurcations and periodic orbits,

see minimal_demo_stst_psol.html, final results in minimal_demo_plot_2dbif.html.

save('minimal_demo_funcs_results.mat')


Published with MATLAB® 7.14