Normal form demo - bifurcation detection and normal form computation

This file is self-contained and requires the extension ddebiftool_extra_nmfm.

$Id$

The system
Initialization
Continuation and plot of steady state branch
Bifurcation detection on the steady state branch
Extracting bifurcation locations
Continuation of the first Hopf branch
Bifurcation detection on the first Hopf branch
The second Hopf branch
Plotting the bifurcations on the branches

The system

This system represents a non-dimensionalized model of two interacting layers of neurons.

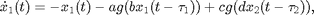
$\dot{x}_1(t) = - x_1(t) - a g(bx_1(t-\tau_1)) + cg (dx_2(t-\tau_2)),$

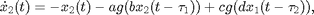
$\dot{x}_2(t) = - x_2(t) - a g(bx_2(t-\tau_1)) + cg (dx_1(t-\tau_2)),$

where 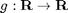$g:\bf{R} \rightarrow \bf{R}$ is of the sigmoidal form

$g(z) = \left[\tanh(z-1) + \tanh(1)\right]\cosh(1)^2.$

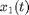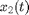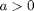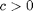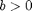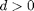The variables $x_1(t)$ and $x_2(t)$ represent the population-averaged neural activity at time $t$ in layers one and two, respectively. The parameter $a > 0$ is a measure of the strength of inhibitory feedback, while $c > 0$ measures the strength of the excitatory effect of one layer on the other. The parameters $b > 0$ and $d > 0$ are saturation rates and the delays 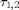$\tau_{1,2}$ represent time lags in the inhibitory feedback loop and excitatory inter-layer connection. Note that the system is symmetric with respect to interchanging the labels $1$ and $2$ , so equilibria are necessarily of the form $(x_0,x_0)$ .

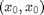Initialization

First, we load the necessary DDE-Biftool extensions. We use existing files in the funcs structure. These files were generated using a Maple script. Lastly, we define the boundaries and step sizes of the active parameters.

clear variables;
close all;
addpath('../../ddebiftool',...
    '../../ddebiftool_extra_psol',...
    '../../ddebiftool_extra_nmfm',...
    '../../ddebiftool_utilities');

funcs=set_funcs(...
    'sys_rhs', @(xx,par) sys_rhs(xx,par),...
    'sys_tau', @() sys_tau(),...
    'sys_deri', @(xx,par,nx,np,v) sys_deri(xx,par,nx,np,v),...
    'sys_mfderi',@(xx,par,varargin) sys_mfderi(xx,par,varargin{:}));

n = 2;

astepsize = 0.0005;
cstepsize = 0.005;
amin = 0.0;
amax = 0.55;
cmin = 0.0;
cmax = 1.0;

Continuation and plot of steady state branch

We set up a steady state branch using SetupStst and do a standard continuation. Then, we plot the branch.

branch1 = SetupStst(funcs,'x',[0;0],'parameter',[0.25, 2, 15/29, 1.2, 12.7, 20.2],...
    'contpar',1,'max_step',[1 astepsize],'max_bound',[1 amax],'min_bound',[1 amin],...
    'newheuristics_tests',0);

branch1.method.continuation.plot = 0;
[branch1,s,f,r] = br_contn(funcs,branch1,300);
branch1 = br_rvers(branch1);
[branch1,s,f,r] = br_contn(funcs,branch1,300);

figure;
[xm,ym] = df_measr(0,branch1,1);
br_plot(branch1,xm,ym);
xlabel('a');
ylabel('x_1');

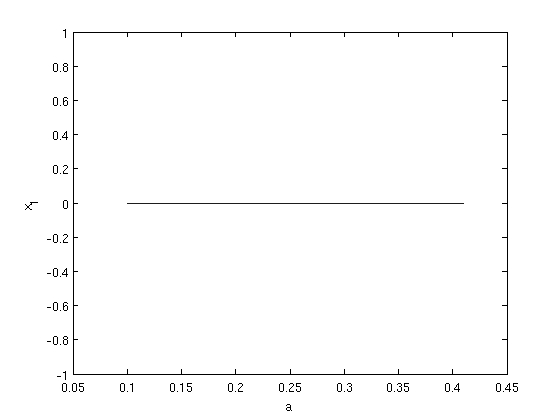
Bifurcation detection on the steady state branch

To detect bifurcations, we have to call the function br_bifdet.

function [newbranch, success] = br_bifdet(funcs, branch)

Inputs:

funcs: problem-definition structure with user-defined functions
branch: branch of steady state (stst) points

Outputs:

newbranch: branch with flagged bifurcation points containing normal form coefficient structures
success: flag whether detection was successful

To adjust the behavior of this algorithm, you can change a number of parameters in branch.method.bifurcation:

minimal_real_part: only roots with a real part above this parameter will be taken into consideration when detecting bifurcations. The default is -0.03. Too many roots will cause overflow (because the hopf detector multiplies them all), so if an overflow is reported, try increasing this parameter.
correction_tolerance: to correct hopf bifurcations, the standard routine p_correc is used. The default value for this corrector is 1e-7.
secant_iterations: codimension 2 bifurcations are corrected using a secant method. This is the maximum number of iterations, with default value 30.
secant_tolerance: this is the tolerance of the secant method, with default 1e-9.
radial_tolerance_factor: after a bifurcation point has been corrected, it is checked whether the corrected point actually lies on the branch. If the bifurcation point originated from a change in the roots between points A and B, the new point is considered "on the branch" if its distance to the line AB is less than 25% of length(AB). This default percentage can be adjusted with this parameter.

You will see some notifications about found hopf points not falling within the branch. This indicates a false positive: the correction algorithm produced a hopf point, but it ended up some distance away from the branch.

branch1.method.bifurcation.minimal_real_part = -0.03;
branch1.method.bifurcation.secant_tolerance=1e-5;
branch1.method.bifurcation.correction_tolerance=1e-5;

fprintf('Bifurcation detection\n');
branch1 = br_bifdet(funcs, branch1);

Bifurcation detection
BR_BIFDET: hopf point found at par(1) = 0.3676281680.
BR_BIFDET: L1 = -0.0028635604, omega = 0.7234938546, par(1) = 0.3676281680.
BR_BIFDET: hopf point found at par(1) = 0.3453112603.
BR_BIFDET: L1 = -0.0133009607, omega = 0.1826428346, par(1) = 0.3453112603.
BR_BIFDET: hopf point found at par(1) = 0.2988605971.
BR_BIFDET: L1 = -0.0054576675, omega = 0.2710841446, par(1) = 0.2988605971.
BR_BIFDET: hopf point found at par(1) = 0.2988605971.
BR_BIFDET: the detected hopf point does not fall within the branch.
BR_BIFDET: hopf point found at par(1) = 0.2988605971.
BR_BIFDET: the detected hopf point does not fall within the branch.

Extracting bifurcation locations

As you can see, three Hopf points were detected. They will have been flagged, e.g. branch1.point(132).flag = 'hopf'. They will also have normal form information: branch1.point(132).nmfm.L1 = -0.0133009607. We will choose two hopf points and continue them. (These two were chosen because their branches happen to intersect, producing a Double Hopf bifurcation.)

To this end, we need to know where the bifurcations were found. We do this by calling br_getflags on the steady state branch.

flagged_point_indices = br_getflags(branch)

Inputs:

branch: any branch

Outputs:

flagged_point_indices: a matrix containing the indices of the bifurcation points in branch.

The way the FPI (flagged point indices) matrix is structured is as follows. Every bifurcation has its own number (0 = stst, 1 = hopf, ...). You can convert between these representations by using string = num2bif(number) and number = bif2num(string). Now, FPI(bif2num('bifucation type'),:) is a list of the indices at which the bifurcation of the designated type occurs. (For the full list, you can refer to any of these two files.)

We first select the second Hopf point on the steady state branch.

FPI = br_getflags(branch1);

start_ind = FPI(bif2num('hopf'),2);

Continuation of the first Hopf branch

We do a standard continuation, using the starting index obtained from the flagged point indices.

fprintf('----- Hopf branch 1 -----\n');
[branch2, suc] = SetupHopf(funcs, branch1, start_ind, 'contpar', [1 3], 'dir', 3, 'step', cstepsize);

branch2.parameter.min_bound=[5 0; 6 0; 3 cmin; 1 amin];
branch2.parameter.max_bound=[1 amax; 3 cmax];
branch2.parameter.max_step=[1 0.002; 3 cstepsize];

branch2.method.continuation.plot = 0;
branch2.method.stability.minimal_time_step = 0.005; % default 0.01

[branch2,s,f,r]=br_contn(funcs,branch2,300);
branch2 = br_rvers(branch2);
[branch2,s,f,r]=br_contn(funcs,branch2,300);

----- Hopf branch 1 -----
BR_CONTN warning: boundary hit.
BR_CONTN warning: boundary hit.

Bifurcation detection on the first Hopf branch

We repeat the steps for bifurcation detection, but now apply it to the hopf branch. This yields several higher-order bifurcations.

branch2.method.bifurcation.minimal_real_part = -0.03;
branch2.method.bifurcation.secant_tolerance=1e-5;
branch2.method.bifurcation.correction_tolerance=1e-5;

branch2 = br_bifdet(funcs,branch2);

BR_BIFDET: zeho point found at par(1) = 0.0037927481, par(3) = 0.8396720010.
BR_BIFDET: omega = 0.1485568996, par(1) = 0.0037927481, par(3) = 0.8396720010.
s = 0.0000855602, theta = 2.0242706451.
BR_BIFDET: hoho point found at par(1) = 0.0899922748, par(3) = 0.7735178974.
BR_BIFDET: omega1 = 0.1560058562, omega2 = 0.2900084424, par(1) = 0.0899922748, par(3) = 0.7735178974.
theta(0) = 1.5255011842, delta(0) = 1.6984697752.
BR_BIFDET: genh point found at par(1) = 0.2566137217, par(3) = 0.6210725697.
BR_BIFDET: L2 = 0.0018108090, omega = 0.1722171486, par(1) = 0.2566137217, par(3) = 0.6210725697.
BR_BIFDET: Unable to correct as hoho point near par(1) = 0.2813.
BR_BIFDET: Unable to correct as zeho point near par(1) = 0.3652.
BR_BIFDET: Unable to correct as hoho point near par(1) = 0.4966.

The second Hopf branch

We now repeat the entire exercise, but with the third hopf point as input.

fprintf('----- Hopf branch 2 -----\n');
FPI = br_getflags(branch1);

start_ind = FPI(bif2num('hopf'),3);
[branch3, suc] = SetupHopf(funcs, branch1, start_ind, 'contpar', [1 3], 'dir', 3, 'step', cstepsize);

branch3.parameter.min_bound=[5 0; 6 0; 3 cmin; 1 amin];
branch3.parameter.max_bound=[1 amax; 3 cmax];
branch3.parameter.max_step=[1 0.002; 3 cstepsize];

branch3.method.continuation.plot = 0;
branch3.method.stability.minimal_time_step = 0.005; % default 0.01

[branch3,s,f,r]=br_contn(funcs,branch3,300);
branch3 = br_rvers(branch3);
[branch3,s,f,r]=br_contn(funcs,branch3,300);

branch3.method.bifurcation.minimal_real_part = -0.03;
branch3.method.bifurcation.secant_tolerance=1e-5;
branch3.method.bifurcation.correction_tolerance=1e-5;
branch3 = br_bifdet(funcs, branch3);

----- Hopf branch 2 -----
BR_CONTN warning: boundary hit.
BR_CONTN warning: boundary hit.
BR_BIFDET: zeho point found at par(1) = 0.0133327150, par(3) = 0.8554382654.
BR_BIFDET: omega = 0.2958015628, par(1) = 0.0133327150, par(3) = 0.8554382654.
s = 0.0000803411, theta = 2.0969328059.
BR_BIFDET: hoho point found at par(1) = 0.0900149247, par(3) = 0.7736041399.
BR_BIFDET: omega1 = 0.2900073517, omega2 = 0.1560072608, par(1) = 0.0900149247, par(3) = 0.7736041399.
theta(0) = 1.6984018466, delta(0) = 1.5254221873.
BR_BIFDET: genh point found at par(1) = 0.2518504300, par(3) = 0.5812203535.
BR_BIFDET: L2 = 0.0011029849, omega = 0.2759107995, par(1) = 0.2518504300, par(3) = 0.5812203535.
BR_BIFDET: Unable to correct as zeho point near par(1) = 0.3348.

Plotting the bifurcations on the branches

We now plot the branches. On the hopf branches, we want to plot the bifurcation points with a special marker. This is done using the function br_bifplot.

function br_bifplot(branch,x_m,y_m,method)

Inputs:

branch: any branch (containing flagged bifurcation points)
x_m: measure for the x-axis
y_m: measure for the y-axis
method: a structure specifying a marker type for all bifurcation types

A default bifurcation plot structure can be obtained with df_bifplot. This function produces a structure that plots all bifurcations with 'o' and steady state points with '-'.

figure;

bifplot = df_bifplot();
bifplot.hoho = '*';

[xm,ym] = df_measr(0,branch2,1);
br_plot(branch2,xm,ym,'-');
br_bifplot(branch2,xm,ym,bifplot);

[xm,ym] = df_measr(0,branch3,1);
br_plot(branch3,xm,ym,'-');
br_bifplot(branch3,xm,ym,bifplot);

br_plot(branch1,xm,ym,'--');

xlabel('a');
ylabel('c');


return;

Normal form demo - bifurcation detection and normal form computation

Contents

The system

Initialization

Continuation and plot of steady state branch

Bifurcation detection on the steady state branch

Extracting bifurcation locations

Continuation of the first Hopf branch

Bifurcation detection on the first Hopf branch

The second Hopf branch

Plotting the bifurcations on the branches