Demo for analysis of phase oscillators with delay

(contributed by Azamat Yeldesbay)

r.h.s. and initial parameters
Integrate to observe rotations
Plot solution time profile
Create functions for ddebiftool
Cut out final full rotation period and create initial piece of branch
Continue branch of rotations
Compute stability
Plot solution profiles and bifurcation diagram of rotations

This demo shows that phase oscillators and rotations can be treated as periodic orbits.

The equation:

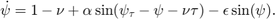
$\dot{\psi} = 1 - \nu + \alpha \sin(\psi_{\tau} - \psi - \nu \tau) - \epsilon \sin(\psi).$

It is a simple model of an oscillator with intrinsic delayed feedback driven by an external periodic force. Parameters of the system are alpha = 1/3, tau = pi, and for nu in [0.5 , 1.5 ], epsilon in [0,0.1]. The rotation solution appears, for example, at alpha=1/3, tau=pi, epsilon=0.02, nu=1.3, or epsilon=0.005 and nu=1. A periodic solution after Hopf bifurcation appears at alpha=1/3, tau=pi, epsilon=0.03, and nu=1.

clear
close all
addpath('../../ddebiftool/',...
    '../../ddebiftool_extra_psol/',...
    '../../ddebiftool_utilities/');

r.h.s. and initial parameters

indnu=1;
indeps=2;
indtau=3;
indalpha=4;
indper=5;
f=@(psi,p)1-p(indnu)+p(indalpha)*sin(psi(1,2,:)-psi(1,1,:)-p(indnu)*p(indtau))-...
    p(indeps)*sin(psi(1,1,:));
par0([indnu,indeps,indtau,indalpha])=[1.3,0.02,pi,1/3];
getp=@(br,ind)arrayfun(@(x)x.parameter(ind),br.point);

Integrate to observe rotations

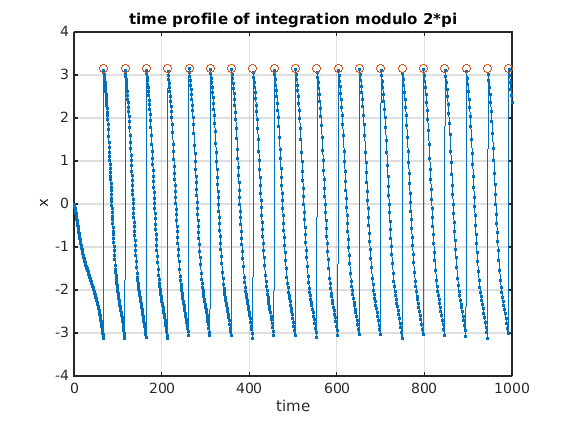
sol23=dde23(@(t,y,z)f([y,z],par0),par0(indtau),0,[0,1000],...
    ddeset('Events',@(t,y,z)cross_pi_dde23(y),'RelTol',1e-6));

Plot solution time profile

figure(1);ax1=gca;
plot(ax1,sol23.x,mod(sol23.y+pi,2*pi)-pi,'.-',sol23.xe,mod(sol23.ye,2*pi),'o');
xlabel(ax1,'time');
ylabel(ax1,'x');
grid(ax1,'on');
title(ax1,'time profile of integration modulo 2*pi');

Create functions for ddebiftool

Note that we add an equation to track the period as an independent parameter (parameter(5))

funcs=set_funcs('sys_rhs',f,'sys_tau',@()indtau,...
    'sys_cond',@(pt)copy_period(pt,indper),'x_vectorized',true);

Cut out final full rotation period and create initial piece of branch

We specify the index of the period as a parameter in the optional argument indperiod. Other ooptinoal parameters are passed on to p_correc.

rot_br=branch_from_sol(funcs,sol23,[indnu,indper],par0,'indperiod',indper,...
    'extra_condition',true,'print_residual_info',1);

it=1, res=0.0207629
it=2, res=1.49643e-05
it=3, res=4.16791e-10
it=1, res=0.120415
it=2, res=0.0158882
it=3, res=0.000144747
it=4, res=5.85404e-09

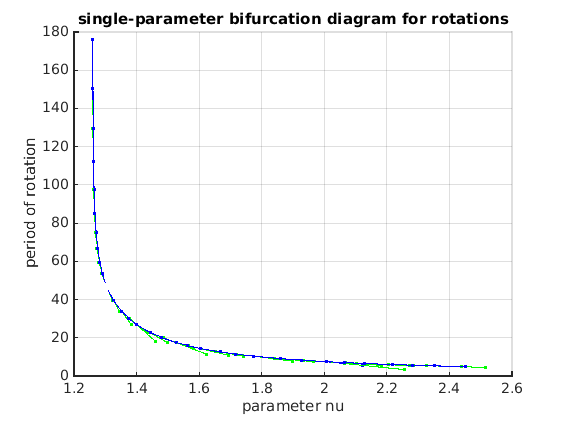
Continue branch of rotations

figure(2);clf;ax2=gca;
xlabel(ax2,'parameter nu');
ylabel(ax2,'period of rotation');
grid(ax2,'on');
title(ax2,'single-parameter bifurcation diagram for rotations');
rot_br=br_contn(funcs,rot_br,30,'plotaxis',ax2);
rot_br=br_rvers(rot_br);
rot_br=br_contn(funcs,rot_br,10,'plotaxis',ax2);
hold(ax2,'off');

it=1, res=0.0369315
it=2, res=0.001123
it=3, res=1.75086e-06
it=4, res=4.0151e-11
it=1, res=0.0606396
it=2, res=0.00355682
it=3, res=1.92371e-05
it=4, res=8.65493e-10
it=1, res=0.000297648
it=2, res=5.39853e-11
it=1, res=0.106307
it=2, res=0.015299
it=3, res=0.000403976
it=4, res=3.73716e-07
it=5, res=8.332e-12
it=1, res=0.197638
it=2, res=0.343365
it=3, res=0.0703184
it=4, res=0.010634
it=5, res=0.00042007
it=1, res=0.0163169
it=2, res=0.000354355
it=3, res=2.43707e-07
it=4, res=5.79448e-12
it=1, res=0.000127758
it=2, res=1.44373e-11
it=1, res=0.0477811
it=2, res=0.00472865
it=3, res=5.07049e-05
it=4, res=9.29968e-09
...

Compute stability

[nunstrot,domrot,triv_defectrot,rot_br.point]=...
    GetStability(rot_br,'funcs',funcs,'exclude_trivial',true);

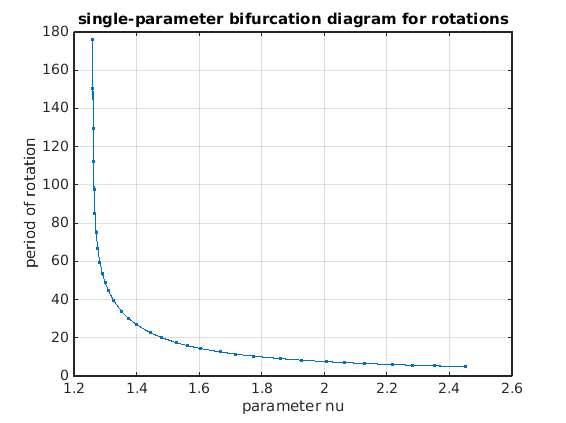
Plot solution profiles and bifurcation diagram of rotations

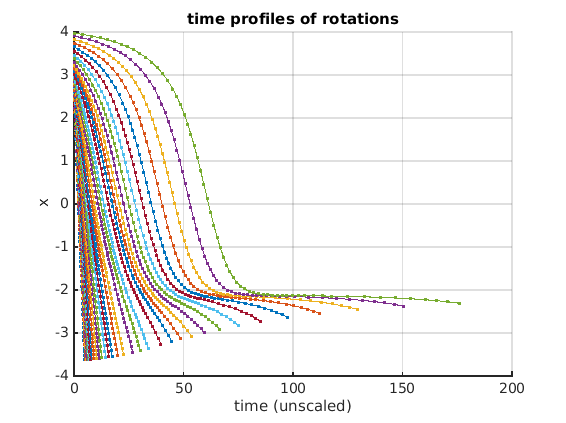
rot_nu=arrayfun(@(x)x.parameter(indnu),rot_br.point);
rot_period=arrayfun(@(x)x.period,rot_br.point);
figure(2);clf;ax2=gca;
plot(rot_nu,rot_period,'.-');
hold(ax2,'off');
xlabel(ax2,'parameter nu');
ylabel(ax2,'period of rotation');
grid(ax2,'on');
title(ax2,'single-parameter bifurcation diagram for rotations');
figure(3);clf;ax3=gca;
hold(ax3,'on');
for i=1:length(rot_nu)
    plot(ax3,rot_br.point(i).mesh*rot_period(i),rot_br.point(i).profile,'.-');
end
hold(ax3,'off');
xlabel(ax3,'time (unscaled)');
ylabel(ax3,'x');
grid(ax3,'on');
title(ax3,'time profiles of rotations');

%save('phase_oscillator_results.mat');