Demo of extension for rotational symmetry using Lang-Kobayashi equations

The equation (modelling a laser subject to delayed coherent optical feedback) is given as

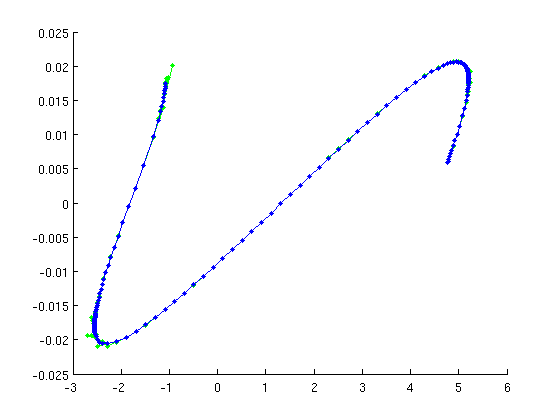
$$E'(t)=[1+i\alpha]n(t)E(t)+\eta\exp(i\phi)E(t-\tau), \qquad n'(t)=\epsilon[p-n(t)-(2n(t)+1)\bar E(t)E(t)]$$

The main bifurcation parameters will be $\eta$ and $\phi$.

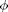Warning The functions for the extended systems determining relative equilibria (rotating waves) and relative periodic orbits (modulated waves), do not have support for user-provided system derivatves or state-dependent delays!

% (c) DDE-BIFTOOL v. 3.1.1(20), 11/04/2014

Contents

Load DDE-Biftool and extension into Path

clear
addpath('../../ddebiftool/',...
    '../../ddebiftool_extra_psol/',...
    '../../ddebiftool_utilities/',...
    '../../ddebiftool_extra_rotsym');

Problem definition using set_rotfuncs

In addition to the user-defined functions set_rotfuncs needs the matrix A generating the rotation and (optional) the rotation as a function 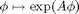$\phi\mapsto \exp(A\phi)$. Then the system is assumed to have rotational symmetry 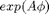$exp(A\phi)$ where A is anti-symmetric.

A=[0,-1,0; 1,0,0; 0,0,0];
expA=@(phi) [cos(phi), -sin(phi),0; sin(phi), cos(phi),0; 0,0,1];

Initial values of parameters and parameter indices

alpha=4;      % alpha factor
pump=0.1;    % injection current
epsilon=5e-3; % carrier relaxation time
eta=5e-3;      % feedback strength
phi0=0;      % feedback phase
tau0=100;      % initial delay
par=[pump,eta,phi0,tau0,alpha,epsilon];
% indices
ndim=3;
ind_pump=1;
ind_eta=2;
ind_phi=3;
ind_tau=4;
ind_omega=length(par)+1;

Right-hand side and call to set_rotfuncs

f=@(x,p)LangKobayashi(x(1,1,:)+1i*x(2,1,:),x(1,2,:)+1i*x(2,2,:),x(3,1,:),...
    p(5),p(ind_pump),p(ind_eta),p(ind_phi),p(6));
rfuncs=set_rotfuncs('sys_rhs',f,'rotation',A,'exp_rotation',expA,...
    'sys_tau',@()ind_tau,'x_vectorized',true);

Extended functions in rotating coordinates for rotating waves

A rotating wave (relative equilibrium, RE) is a solution of the form

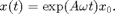
$$ x(t)=\exp(A\omega t)x_0. $$

The extended functions in rfuncs will always treat the user-provided system in rotating coordinates.

Original system (by user):

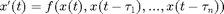
$$x'(t)=f(x(t),x(t-\tau_1),...,x(t-\tau_n))$$

Rotating coordinates: 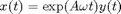$x(t)=\exp(A\omega t)y(t)$:

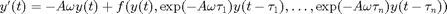
$$y'(t)=-A \omega y(t)+f(y(t),\exp(-A\omega\tau_1)y(t-\tau_1),\ldots, \exp(-A\omega\tau_n)y(t-\tau_n))$$

The rotation speed is chosen such that the rotating wave 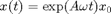$x(t)=\exp(A\omega t)x_0$ is turned into an equilibrium 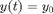$y(t)=y_0$. This is achieved by solving for equilibria of the $y$ equation and adding a sys_cond (file rot_cond.m) to povide an equation determining $\omega$. For rotating waves this is

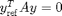
$$ y_\mathrm{ref}^TAy=0 $$

As DDE-Biftool does not give the user's sys_cond access to reference points, rot_cond returns residual 0 and Jacobian 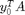$y_0^TA$.

Initial guess

The extension for rotating and modulated waves is not able to cope with invariant equilibria. Thus, we generate a non-trivial rotating wave as our initial guess. For the laser the rotating waves correspond to stationary lasing (on state) 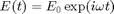$E(t)=E_0\exp(i\omega t)$, $n=n_0$.

[E0,n0,phi0,omega0]=LK_init(alpha,pump,eta,tau0);
par(ind_phi)=phi0;
par(ind_omega)=omega0;
opt_inputs={'extra_condition',1,'print_residual_info',0};

Relative equilibria varying phase phi of the delayed feedback

The standard convenience function SetupStst works, but one must add the continuation parameter index length(parameter) to the index list of continuation parameters.

Warning DDE-Biftool assumes that the rotation speed is the last parameter in the parameter vector!

rw_phas=SetupStst(rfuncs,'contpar',[ind_phi,ind_omega],'corpar',ind_omega,...
    'x',[E0;n0],'parameter',par,opt_inputs{:},...
    'max_step',[ind_phi,0.2]);
figure(2);clf
rw_phas=br_contn(rfuncs,rw_phas,200);

Linear Stability of relative equilibria

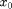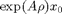The standard convenience function GetStability works. However, all relative equilibria have a trivial eigenvalue 0, corresponding to phase shift. If $x_0$ is a relative equilibrium (with rotation speed $\omega$) then $\exp(A\rho)x_0$ is also a relative equilibrium with the same rotation speed $\omega$. One can adapt GetStability by setting the optional flag exclude_trivial to true and providing a function for locating the trivial eigenvalue: 'locate_trivial',@(p)0.

[rw_phas_nunst,dom,defect,rw_phas.point]=GetStability(rw_phas,...
    'exclude_trivial',true,'locate_trivial',@(p)0,'funcs',rfuncs);
% plot with stability information
p2=arrayfun(@(p)p.parameter(ind_phi),rw_phas.point);
A2=arrayfun(@(p)norm(p.x(1:2)),rw_phas.point);
n2=arrayfun(@(p)norm(p.x(3)),rw_phas.point);
om2=arrayfun(@(p)p.parameter(ind_omega),rw_phas.point);
figure(1);clf
tdeco={'fontsize',14,'fontweight','bold'};
sel=@(x,i)x(rw_phas_nunst==i);
plot(sel(p2,0),sel(A2,0),'k.',sel(p2,1),sel(A2,1),'r.',...
    sel(p2,2),sel(A2,2),'c.',sel(p2,3),sel(A2,3),'b.','linewidth',2);
% detect Hopf bifurcations
ind_hopf=find(abs(diff(rw_phas_nunst))==2);
hold on
plot(p2(ind_hopf),A2(ind_hopf),'ks','linewidth',2);
hold off
set(gca,tdeco{:});
xlabel('phi',tdeco{:});
ylabel('|E|',tdeco{:});

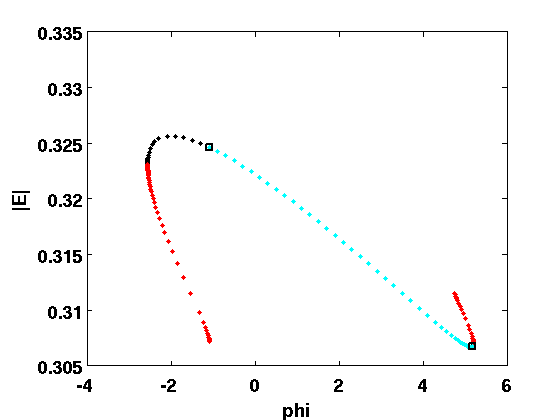
Modulated waves (Relative periodic orbits, RPOs)

Modulated waves are solutions of the form

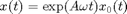
$$ x(t)=\exp(A\omega t)x_0(t)$$

where 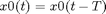$x0(t)=x0(t-T)$ for all $t$ and some period 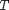$T$. That is, 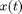$x(t)$ is quasi-periodic, but can be turned into a periodic solution in rotating coordinates. The transformation to rotating coordinates is the same as for relative equilibria, but the additional condition (rot_cond) is

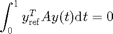
$$\int_0^1 y_\mathrm{ref}^TAy(t) \mathrm{d} t=0$$

where 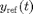$y_\mathrm{ref}(t)$ is a reference solution. Since DDE-Biftool does not give access to reference solutions in user-defined conditions, rot_cond returns residual 0 and Jacobian $y(t)^TA$.

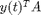RPOs branching off at 2nd Hopf of REs

The initialization works with the standard routine. Again, the rotation speed needs to be added to the list of continuation parameters.

[rw_phas_per,suc]=SetupPsol(rfuncs,rw_phas,ind_hopf(2),opt_inputs{:},...
    'max_step',[ind_phi,0.1],'print_residual_info',1,'radius',0.02);
if ~suc
    error('Hopf initialization failed');
end
figure(2);clf
rw_phas_per=br_contn(rfuncs,rw_phas_per,120);

it=1, res=0.000477416
it=2, res=3.6662e-06
it=3, res=5.22068e-10
it=1, res=0.0221118
it=2, res=1.03329e-05
it=3, res=1.89367e-10
it=1, res=5.30159e-05
it=2, res=8.06852e-12
it=1, res=0.0588672
it=2, res=0.00783925
it=3, res=0.000225981
it=4, res=1.17327e-07
it=5, res=1.68753e-11
it=1, res=0.0150051
it=2, res=0.000562676
it=3, res=8.21825e-07
it=4, res=3.38499e-11
it=1, res=6.52136e-05
it=2, res=5.3547e-11
it=1, res=0.0114482
...

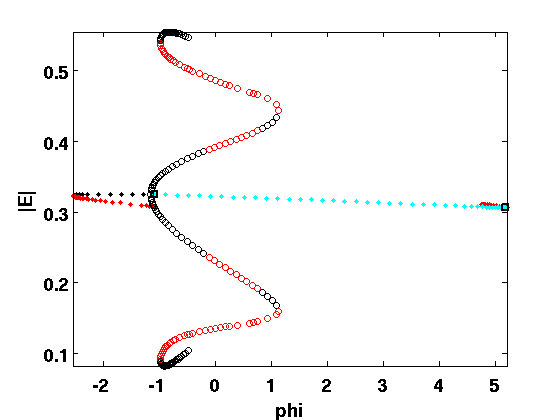
Stability of RPOs

Similar to REs, the RPOs have an additional trivial Floquet multiplier 1. That is, overall, RPOs have always a double Floquet multiplier 1. To exclude the two Floquet mulitpliers closest to unity from the stability, set the optional flag 'exclude_trivial' to true and provide for the optional argument 'locate_trivial' the function @(p)[1,1].

[rw_phas_per_nunst,dom_per,defect,rw_phas_per.point]=GetStability(rw_phas_per,...
    'exclude_trivial',true,'locate_trivial',@(p)[1,1],'funcs',rfuncs);
% plot with stability info
pp=arrayfun(@(p)p.parameter(ind_phi),rw_phas_per.point);
Epow=@(x)sqrt(sum(x(1:2,:).^2,1));
Apmx=arrayfun(@(p)max(Epow(p.profile)),rw_phas_per.point);
Apmn=arrayfun(@(p)min(Epow(p.profile)),rw_phas_per.point);
figure(1);hold on
sel=@(x,i)x(rw_phas_per_nunst==i);
plot(sel(pp,0),[sel(Apmx,0);sel(Apmn,0)],'ko',...
    sel(pp,1),[sel(Apmx,1);sel(Apmn,1)],'ro');
axis tight

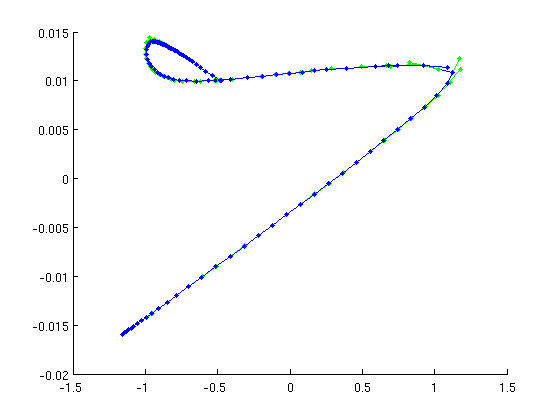
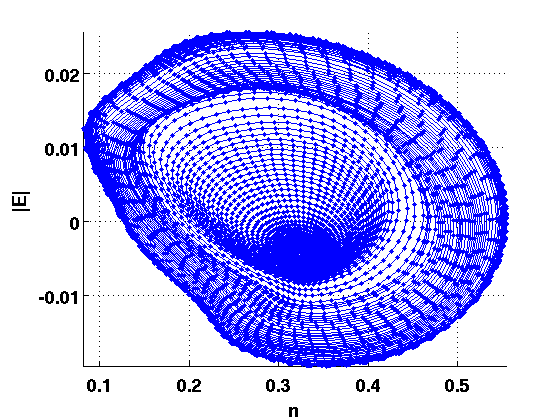
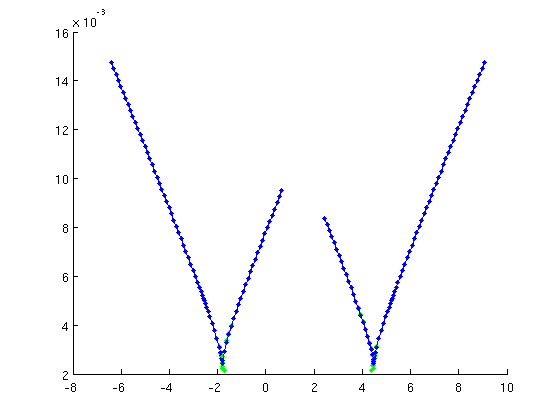
Plot of "phase portraits" of relative periodic orbits

figure(2);clf;hold on
for i=1:length(rw_phas_per.point)
    plot(Epow(rw_phas_per.point(i).profile),rw_phas_per.point(i).profile(3,:),'.-');
end
hold off
grid on
axis tight
set(gca,tdeco{:});
xlabel('n',tdeco{:});
ylabel('|E|',tdeco{:});

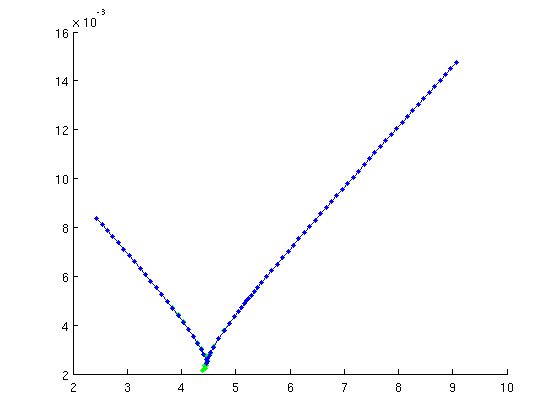
Continuation of fold of relative equilibria

The functions for the extended system are generated by SetupRWFold. The standard routine SetupPOfold has to be modified because the extended condition rot_cond has to be applied to the derivative, too. Also the rotation speed needs to be added to the list of continuation parameters. The extended system for fold continuation of REs has one additional artificial continuation parameter.

ind_fold=find(abs(diff(rw_phas_nunst))==1);
[foldfuncs,fold1branch,suc]=SetupRWFold(rfuncs,rw_phas,ind_fold(1),...
    'contpar',[ind_phi,ind_eta,ind_omega],opt_inputs{:},...
    'print_residual_info',1,'dir',ind_eta,'step',1e-4,...
    'max_step',[ind_phi,0.1; ind_eta,0.01]);
%
figure(2);clf
fold1branch=br_contn(foldfuncs,fold1branch,40);
fold1branch=br_rvers(fold1branch);
fold1branch=br_contn(foldfuncs,fold1branch,40);

it=1, res=0.000227057
it=2, res=1.89309e-07
it=3, res=7.55566e-13
it=1, res=0.00295185
it=2, res=3.1161e-05
it=3, res=1.17747e-09
it=4, res=1.48714e-13
it=1, res=0.000121684
it=2, res=4.67372e-08
it=3, res=1.17521e-12
it=1, res=0.000167978
it=2, res=7.92878e-08
it=3, res=2.02029e-12
it=1, res=0.000230893
it=2, res=1.32172e-07
it=3, res=3.39468e-12
it=1, res=0.000316131
it=2, res=2.15835e-07
it=3, res=5.57805e-12
it=1, res=0.00043142
...

Continuation of 2nd fold of relative equilibria

[foldfuncs,fold2branch,suc]=SetupRWFold(rfuncs,rw_phas,ind_fold(2),...
    'contpar',[ind_phi,ind_eta,ind_omega],opt_inputs{:},...
    'print_residual_info',1,'dir',ind_eta,'step',1e-4,...
    'max_step',[ind_phi,0.1; ind_eta,0.01]);
fold2branch=br_contn(foldfuncs,fold2branch,40);
fold2branch=br_rvers(fold2branch);
fold2branch=br_contn(foldfuncs,fold2branch,40);

it=1, res=0.0015423
it=2, res=6.08298e-06
it=3, res=8.11908e-11
it=1, res=0.00260918
it=2, res=1.77492e-05
it=3, res=1.04899e-09
it=4, res=1.27337e-13
it=1, res=8.39014e-05
it=2, res=3.18751e-08
it=3, res=7.03865e-13
it=1, res=0.000113958
it=2, res=5.685e-08
it=3, res=1.16332e-12
it=1, res=0.000153584
it=2, res=9.80475e-08
it=3, res=1.85983e-12
it=1, res=0.000205308
it=2, res=1.63672e-07
it=3, res=2.86437e-12
it=1, res=0.000272155
...

Continuation of Hopf bifurcations of relative equilibria

For Hopf bifurcation continuation the standard routine SetupHopf works without modification (SetupRWHopf is a simple wrapper).

[h1branch,suc]=SetupRWHopf(rfuncs,rw_phas,ind_hopf(1),...
    'contpar',[ind_phi,ind_eta,ind_omega],opt_inputs{:},...
    'print_residual_info',1,'dir',ind_eta,'step',1e-4,'minimal_accuracy',1e-4);
h1branch=br_contn(rfuncs,h1branch,50);
h1branch=br_rvers(h1branch);
h1branch=br_contn(rfuncs,h1branch,50);

it=1, res=0.000130178
it=2, res=3.07845e-07
it=3, res=1.14108e-11
it=1, res=0.000104569
it=2, res=2.39606e-07
it=3, res=4.63018e-12
it=1, res=1.05922e-06
it=2, res=1.9842e-10
it=3, res=6.53449e-13
it=1, res=1.51752e-06
it=2, res=4.03755e-10
it=3, res=5.98634e-13
it=1, res=2.18395e-06
it=2, res=8.18019e-10
it=3, res=4.11993e-13
it=1, res=3.15694e-06
it=2, res=1.65164e-09
it=3, res=1.01893e-12
it=1, res=4.59929e-06
it=2, res=3.32749e-09
...

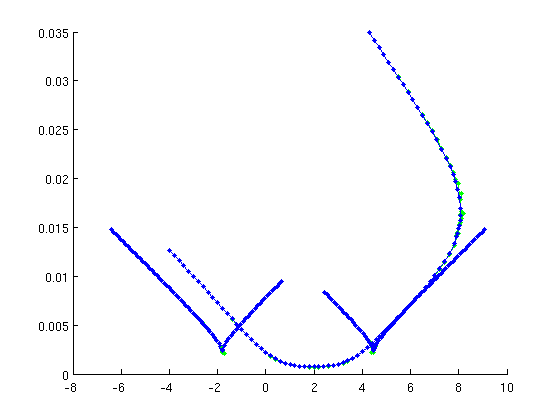
Plot all bifurcations of relative equilibria

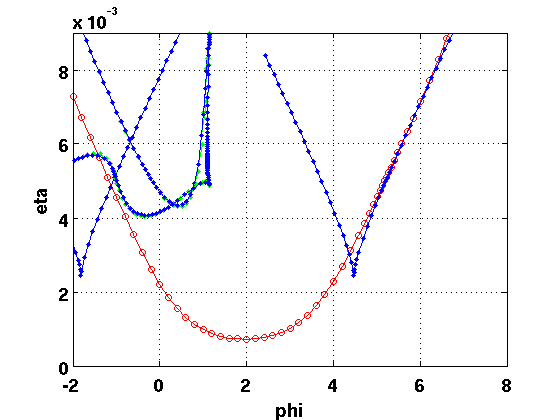
getpar=@(ip,br)arrayfun(@(x)x.parameter(ip),br.point);
ph=getpar(ind_phi,h1branch);
eh=getpar(ind_eta,h1branch);
pf=getpar(ind_phi,fold1branch);
ef=getpar(ind_eta,fold1branch);
pf2=getpar(ind_phi,fold2branch);
ef2=getpar(ind_eta,fold2branch);
figure(2);clf
plot(ph,eh,'ro-', pf,ef,'b.-', pf2,ef2,'b.-');
axis([-2,8,0,0.009]);
grid on
set(gca,tdeco{:});
xlabel('phi',tdeco{:});
ylabel('eta',tdeco{:});

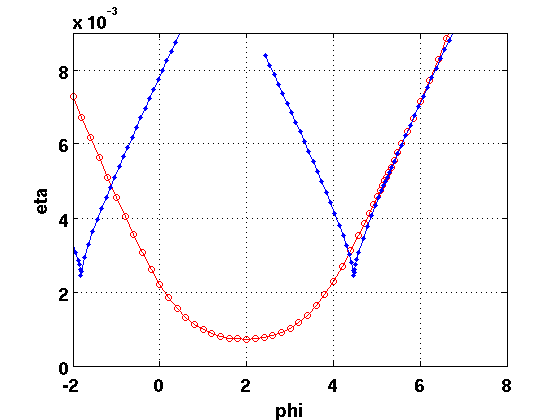
Period doubling of relative POs

The standard initialization works (wrapped to give it sensible name). The rotation speed needs to be added to the list of continuation parameters.

ind_pd=find(diff(rw_phas_per_nunst)==1&dom_per(1:end-1)<0);
[pdfuncs,pdbr]=SetupMWPeriodDoubling(rfuncs,rw_phas_per,ind_pd,...
    'contpar',[ind_phi,ind_eta,ind_omega],opt_inputs{:},...
    'print_residual_info',1,'dir',ind_eta,'step',1e-4);

it=1, res=0.544434
it=2, res=0.0117503
it=3, res=7.96708e-06
it=4, res=6.67635e-11
it=1, res=0.021419
it=2, res=6.5234e-09
it=1, res=0.154902
it=2, res=0.00731031
it=3, res=8.8049e-06
it=4, res=9.55255e-10
it=1, res=0.00387263
it=2, res=8.19995e-10

figure(2);
pdbr=br_contn(pdfuncs,pdbr,20);
pdbr=br_rvers(pdbr);
pdbr=br_contn(pdfuncs,pdbr,20);

it=1, res=0.0201666
it=2, res=3.31718e-05
it=3, res=6.2154e-10
it=1, res=0.0253107
it=2, res=5.9337e-05
it=3, res=1.20822e-09
it=1, res=0.0100943
it=2, res=2.36606e-09
it=1, res=0.0351951
it=2, res=0.000102233
it=3, res=2.5438e-09
it=1, res=0.0370704
it=2, res=0.00014216
it=3, res=2.53427e-09
it=1, res=0.0345254
it=2, res=0.000130282
it=3, res=3.54583e-09
it=1, res=0.00839129
it=2, res=2.19358e-09
it=1, res=0.032157
...

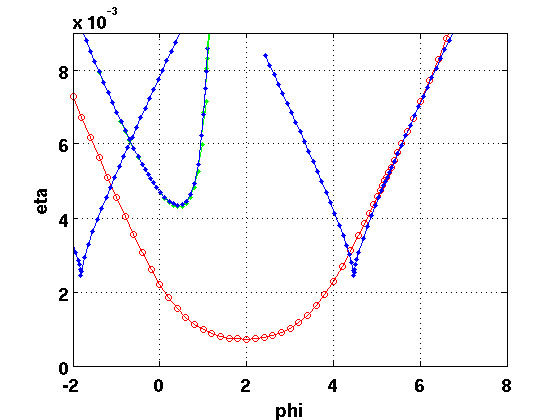
Stability of orbits at the period doubling

Here the stability includes the Floquet multiplier -1. Alternatively include -1 into the list in 'locate_trivial': 'locate_trivial',@(p)[1,1,-1].

pdorbs=pdfuncs.get_comp(pdbr.point,'solution');
[nunst_pd,dom,triv_defect,pdorbs]=GetStability(pdorbs,...
    'exclude_trivial',true,'locate_trivial',@(p)[1,1],'funcs',rfuncs); %#ok<*ASGLU>
fprintf('max error of Floquet mult close to -1: %g\n',max(abs(dom+1)));

max error of Floquet mult close to -1: 5.32865e-05

Fold of relative POs

Folds of RPOs require a modified initialization routine since the condition rot_cond needs to be applied to the derivative, too. This requires again the introduction of an artificial parameter (automatically appended to parameter vector). Theuser has to add rotation speed to the list of continuation parameters.

ind_mwf=find(diff(rw_phas_per_nunst)==1&dom_per(1:end-1)>0)+1;
[pfoldfuncs,mwfoldbr]=SetupMWFold(rfuncs,rw_phas_per,ind_mwf(1),...
    'contpar',[ind_phi,ind_eta,ind_omega],opt_inputs{:},...
    'print_residual_info',1,'dir',ind_eta,'step',1e-4);

it=1, res=0.00883104
it=2, res=0.00131223
it=3, res=6.64663e-06
it=4, res=3.52906e-10
it=1, res=0.0135664
it=2, res=1.38763e-08
it=3, res=3.10375e-12
it=1, res=0.0485972
it=2, res=0.00701452
it=3, res=0.000235835
it=4, res=1.89466e-07
it=5, res=3.70301e-12
it=1, res=0.00853501
it=2, res=7.53072e-09

figure(2);
mwfoldbr=br_contn(pfoldfuncs,mwfoldbr,80);
mwfoldbr=br_rvers(mwfoldbr);
mwfoldbr=br_contn(pfoldfuncs,mwfoldbr,60);

it=1, res=0.0169774
it=2, res=0.0101654
it=3, res=0.0124415
it=1, res=0.00469105
it=2, res=1.00458e-05
it=3, res=8.32561e-10
it=1, res=0.00515276
it=2, res=4.71748e-09
it=1, res=0.0075479
it=2, res=0.000335056
it=3, res=4.59115e-06
it=4, res=1.06217e-09
it=1, res=0.010977
it=2, res=1.25696
it=3, res=0.369966
it=4, res=0.0789973
it=5, res=0.021356
it=1, res=0.00103736
it=2, res=2.3066e-05
it=3, res=1.00884e-08
...

Stability of orbits at fold of RPOs

Here the stability includes the Floquet multiplier -1. Alternatively include another 1 into the list in 'locate_trivial': 'locate_trivial',@(p)[1,1,1].

mwforbs=pfoldfuncs.get_comp(mwfoldbr.point,'solution');
[nunst_mwf,dom,triv_defect,mwforbs]=GetStability(mwforbs,...
    'exclude_trivial',true,'locate_trivial',@(p)[1,1],'funcs',rfuncs);
fprintf('max error of Floquet mult close to -1: %g\n',max(abs(dom-1)));

max error of Floquet mult close to -1: 0.30039

save('LKbifs.mat');

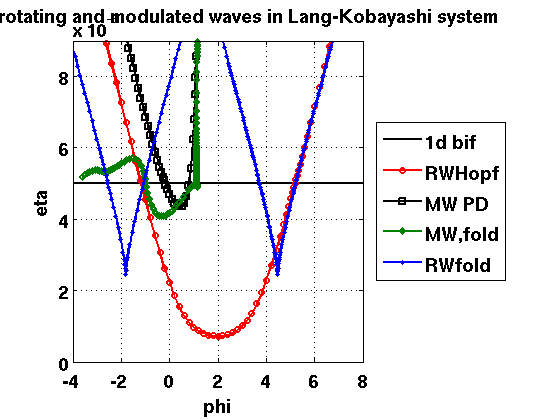
re-plot all bifurcations

plot_2dbifs;


Published with MATLAB® 7.14