DDE-BIFTOOL state-dependent delays sd-demo

This demo is an illustrative example, showing how to perform bifurcation analysis for a system with state-dependent delays.

The demo shows

which functions the user has to provide and how to put them into the structure funcs (sd_demo_funcs.html)
continuation of equilibria and their linear stability sd_demo_stst.html,
detection and continuation of Hopf bifurcations sd_demo_hopf.html,
branching off from Hopf bifurcation and continuation of periodic orbits sd_demo_psol.html

% (c) DDE-BIFTOOL v. 3.1.1(20), 11/04/2014

Differential equations
First step: the definition of user-defined functions, see sd_demo_funcs.html

Differential equations

The differential equations for this example are

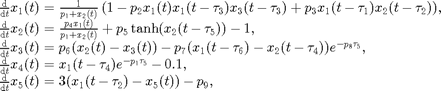
$\begin{array}{l} \frac{\mathrm{d}}{\mathrm{d} t}x_1(t)=\frac{1}{p_1+x_2(t)}\left(1-p_2x_1(t)x_1(t-\tau_3) x_3(t-\tau_3)+p_3x_1(t-\tau_1)x_2(t-\tau_2)\right),\\ \frac{\mathrm{d}}{\mathrm{d} t}x_2(t)=\frac{p_4 x_1(t)}{p_1+x_2(t)}+ p_5\tanh(x_2(t-\tau_5))-1,\\ \frac{\mathrm{d}}{\mathrm{d} t}x_3(t)=p_6(x_2(t)-x_3(t))-p_7(x_1(t-\tau_6)-x_2(t-\tau_4))e^{-p_8 \tau_5},\\ \frac{\mathrm{d}}{\mathrm{d} t}x_4(t)=x_1(t-\tau_4)e^{-p_1 \tau_5} -0.1,\\ \frac{\mathrm{d}}{\mathrm{d} t}x_5(t)=3(x_1(t-\tau_2)-x_5(t))-p_9, \end{array}$

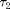where $\tau_1$ and $\tau_2$ are constant delays and

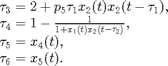
$\begin{array}{l} \tau_3=2+p_5\tau_1x_2(t)x_2(t-\tau_1),\\ \tau_4=1-\frac{1}{1+x_1(t)x_2(t-\tau_2)},\\ \tau_5=x_4(t),\\ \tau_6=x_5(t). \end{array}$

This system has five components 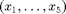$(x_1,\ldots,x_5)$ , six delays $(\tau_1,\ldots,\tau_6)$ and eleven parameters $(p_1,\ldots,p_{11})$ , where $p_{10}=\tau_1$ and $p_{11}=\tau_2$ .

clear;                           % clear variables
close all;                       % close figures
addpath('../../ddebiftool/');    % add ddebiftool folder to path
%#ok<*ASGLU,*NOPTS,*NASGU>

DDE-BIFTOOL state-dependent delays sd-demo

Contents

Differential equations

First step: the definition of user-defined functions, see sd_demo_funcs.html