User-provided partial derivatives of state-dependent delays

Implementation for tutorial demo neuron:

function dtau=sd_dtau(k,xx,par,nx,np)

Inputs

k (integer): the index k of the delay for which the derivative is requested
xx (array with sys_ntau()+1 columns): values of states $[x(t),\ldots,x(t-\tau_k),\ldots,x(t-\tau_n)]$
par: row vector of system parameters
nx (integer or vector of two integers): index wrt which element of xx 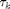$\tau_k$ has to be differentiated
np (integer): index wrt to which element of par 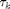$\tau_k$ has to be differentiated

Output dtau: partial derivative of 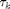$\tau_k$ wrt

xx(:,nx) if nx is scalar and np is empty (dtau is row vector of length size(xx,1)),
par(:,np) if nx is empty and np is scalar (dtau is scalar),
xx(:,nx(1)) and xx(nx(2) if nx has length2 and np is empty (|dtau is square matrix of size(xx,1)),
xx(:,nx(1)) and par(np if nx and np have length 1 (|dtau is row vector of length size(xx,1)).

If a user-provided function sys_dtau is not provided, DDE-Biftool will use finite-difference approximation (implemented in df_derit.m).

% (c) DDE-BIFTOOL v. 3.1.1(20), 11/04/2014

Parameter vector
first order derivatives wrt state variables:
First order derivatives wrt parameters
Second order derivatives wrt state variables
Mixed state parameter derivatives
Otherwise raise error

function dtau=sd_dtau(delay_nr,xx,par,nx,np)

Parameter vector

p1 p2 p3 p4 p5 p6 p7 p8 p9 p10 p11

n=size(xx,1);
nvec=size(xx,3);
if length(nx)==1 && isempty(np)

first order derivatives wrt state variables:

    dtau=zeros(1,n,nvec);
    if nx==0 % derivative wrt x(t)
        if delay_nr==3
            dtau(1,2,:)=par(5)*par(10)*xx(2,2,:);
        elseif delay_nr==4
            dtau(1,1,:)=xx(2,3,:)./(1+xx(1,1,:).*xx(2,3,:)).^2;
        elseif delay_nr==5
            dtau(1,4,:)=1;
        elseif delay_nr==6
            dtau(1,5,:)=1;
        end
    elseif nx==1 % derivative wrt x(t-tau1)
        if delay_nr==3
            dtau(1,2,:)=par(5)*par(10)*xx(2,1,:);
        end
    elseif nx==2 % derivative wrt x(t-tau2)
        if delay_nr==4
            dtau(1,2,:)=xx(1,1,:)./(1+xx(1,1,:).*xx(2,3,:)).^2;
        end
    end

elseif isempty(nx) && length(np)==1,

First order derivatives wrt parameters

    dtau=zeros(1,nvec);
    if delay_nr==1 && np==10
        dtau(1,:)=1;
    elseif delay_nr==2 && np==11
        dtau(1,:)=1;
    elseif delay_nr==3 && np==5
        dtau(1,:)=par(10)*xx(2,1,:).*xx(2,2,:);
    elseif delay_nr==3 && np==10
        dtau(1,:)=par(5)*xx(2,1,:).*xx(2,2,:);
    end

elseif length(nx)==2 && isempty(np),

Second order derivatives wrt state variables

    dtau=zeros(n,n,nvec);
    if delay_nr==3
        if (nx(1)==0 && nx(2)==1) || (nx(1)==1 && nx(2)==0)
            dtau(2,2,:)=par(5)*par(10);
        end
    elseif delay_nr==4
        if nx(1)==0 && nx(2)==0
            dtau(1,1,:)=-2*xx(2,3,:).*xx(2,3,:)./(1+xx(1,1,:)*xx(2,2,:)).^3;
        elseif nx(1)==0 && nx(2)==2
            dtau(1,2,:)=(1-xx(1,1,:).*xx(2,3,:))./(1+xx(1,1,:).*xx(2,2,:)).^3;
        elseif nx(1)==2 && nx(2)==0
            dtau(2,1,:)=(1-xx(1,1,:).*xx(2,3,:))./(1+xx(1,1,:).*xx(2,2,:)).^3;
        elseif nx(1)==2 && nx(2)==2
            dtau(2,2,:)=-2*xx(1,1,:).*xx(1,1,:)./(1+xx(1,1,:).*xx(2,2,:)).^3;
        end
    end

elseif length(nx)==1 && length(np)==1,

Mixed state parameter derivatives

    dtau=zeros(1,n,nvec);
    if delay_nr==3
        if nx==0 && np==5
            dtau(1,2,:)=par(10)*xx(2,2,:);
        elseif nx==0 && np==10
            dtau(1,2,:)=par(5)*xx(2,2,:);
        elseif nx==1 && np==5
            dtau(1,2,:)=par(10)*xx(2,1,:);
        elseif nx==1 && np==10
            dtau(1,2,:)=par(5)*xx(2,1,:);
        end
    end

end

Otherwise raise error

Raise error if the requested derivative does not exist

if isempty(dtau)
    error(['SYS_DTAU, delay %d: requested derivative ',...
        'nx=%d, np=%d does not exist!'],delay_nr, nx, np);
end

end