DDE-BIFTOOL demo 1 - Neuron

This demo is an illustrative example, which uses a system of delay differential equations taken from [Shay,99].

The demo will show

which functions the user has to provide and how to put them into the structure funcs (demo1_funcs.html)
continuation of equilibria in a single parameter, demo1_stst.html
computation of their stability (eigenvalues of linearization), demo1_stst.html
continuation of Hopf bifurcations in two parameters (demo1_hopf.html)
computation of normal form coefficients for Hopf bifurcations (to check if they are supercritical or subcritical), and of normal form coefficients for codimension-two bifurcations encountered along Hopf curves (demo1_normalforms.html),
branching off from a Hopf bifurcation to continue a family of periodic orbits in a single parameter demo1_psol.html
computation of stability of periodic orbits (Floquet multipliers of linearization) demo1_psol.html
continuation of homoclinic connections in two parameters demo1_hcli.html
continuation of folds of periodic orbits in two parameters demo1_POfold.html

Differential equations
First step: the definition of user-defined functions, see demo1_funcs.html

Differential equations

The differential equations for this example are

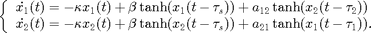
$\left\{\begin{array}{l}\dot{x_1}(t)= -\kappa x_1(t)+\beta \tanh(x_1(t-\tau_s))+a_{12}\tanh(x_2(t-\tau_2)) \\ \dot{x_2}(t)=-\kappa x_2(t)+\beta \tanh(x_2(t-\tau_s))+a_{21}\tanh(x_1(t-\tau_1)). \end{array}\right.$

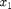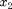This system models two coupled neurons with time delayed connections. It has two components ( $x_1$ and $x_2$ ), three delays ( $\tau_1$ , $\tau_2$ and $\tau_s$ ), and four other parameters ( 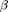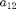$\kappa$ , $\beta$ , $a_{12}$ and $a_{21}$ ).

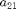The primary bifurcation parameter will be 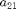$a_{21}$ the second parameter is $\tau_s$ .

clear;                           % clear variables
format compact
close all;                       % close figures
addpath('../../ddebiftool/');    % add ddebiftool folder to path
%#ok<*ASGLU,*NOPTS,*NASGU>

DDE-BIFTOOL demo 1 - Neuron

Contents

Differential equations

First step: the definition of user-defined functions, see demo1_funcs.html