Definition of user functions

(Please load ddebiftool into path first, see demo1.html.) To define a system, the user should provide Matlab functions defining the right-hand side (in the example called neuron_sys_rhs) and the indices for the delays in the parameter vector (called neuron_tau in our example).

Right-hand side
Delays
Jacobians of user-provided functions
Definition of structure funcs
Save and continue to continuation and stability of steady states demo1_stst.html

Right-hand side

A function defining the right-hand side 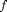$f$ :

function y=sys_rhs(xx,par)

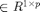This function has two arguments, xx $\in R^{n\times (m+1)}$ , which contains the state variable(s) at the present and in the past, xx $=[x(t), x(t-\tau_1), \ldots, x(t-\tau_m)]$ , par $\in R^{1\times p}$ which contains the parameters, par $=\eta$ .

For the example, this is (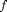 $f$ is called neuron_sys_rhs in our example)

neuron_sys_rhs=@(xx,par)[...
    -par(1)*xx(1,1)+par(2)*tanh(xx(1,4))+par(3)*tanh(xx(2,3));....
    -par(1)*xx(2,1)+par(2)*tanh(xx(2,4))+par(4)*tanh(xx(1,2))];

Delays

The delays $\tau_i$ , $i=1\ldots,m$ are considered to be part of the parameters (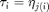 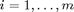$\tau_i=\eta_{j(i)}$ , $i=1,\ldots,m$ ). This is natural since the stability of steady solutions and the position and stability of periodic solutions depend on the values of the delays. Furthermore delays can occur both as a 'physical' parameter and as delay, as in $\dot{x}=\tau x(t-\tau)$ . 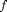From these inputs the right-hand side $f$ is evaluated at time $t$ . For equations with constant delays DDE-Biftool determines which parameters are delays by calling an argument-less function of the type

function d=sys_tau()

In the example we order the parameters as par $=[\kappa, \beta, a_{12}, a_{21},\tau_1,\tau_2, \tau_s]$ . Thus, (giving it the name neuron_tau):

neuron_tau=@()[5,6,7];
ind_a21=4;  % used later for continuation
ind_taus=7; % used later for continuation

Jacobians of user-provided functions

Optionally (recommended) the user may also specify the partial derivatives of the user-defined functions with respect to states, delayed states and parameters. For constant delays only the derivatives of 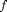$f$ are required. They should be provided as a function of the form

function J=sys_deri(xx,par,nx,np,v)

providing the partial derivatives of first and second order (see file neuron_sys_deri.html for details).

Definition of structure `funcs`

Similar to standard functions such as ode45 DDE-Biftool's routines now have an argument that defines the right-hand side. Since DDE-Biftool needs several user-defined functions (sys_rhs, sys_tau, optionally sys_deri, sys_cond etc) these functions are collected in a structure funcs. This structure funcs is best set up by calling the (new) DDE-Biftool routine set_funcs wit a sequence of name-value pairs. Each name-value pair corresponds to a field in the structure. Fields that are not listed as arguments of set_funcs get replaced by a default if possible.

Possible argument names are:

'sys_rhs' (default sys_rhs if file sys_rhs.m present in folder): right-hand side sys_tau
'sys_tau' (default @()[]): function defining delays
'sys_deri' (default @df_deriv): function defining partial derivatives of sys_rhs
'sys_ntau' (default 0, only needed for state-dependent delays) number of delays
'sys_cond' (default @dummy_cond) function providing extra conditions
'sys_dtau' (default @df_derit, only needed for state-dependent delays): function defining partial derivatives of sys_tau
'x_vectorized' (logical, default false) set to true if sys_rhs, sys_deri, (sys_tau and sys_dtau for SD-DDEs) accept an argument xx with three dimensions. For periodic-orbit computations the function will be called with all collocation points simultaneously if x_vectorized is true.

Other fields are tp_del (true if delays are state-dependent), sys_deri_provided (true if user has provided sys_deri) and sys_dtau_provided (true if user has provided sys_dtau).

funcs=set_funcs(...
    'sys_rhs',neuron_sys_rhs,...
    'sys_tau',@()[5,6,7],...
    'sys_deri',@neuron_sys_deri) %#ok<NOPTS>

funcs = 
                sys_rhs: [function_handle]
               sys_ntau: @()0
                sys_tau: @()[5,6,7]
               sys_cond: @dummy_cond
               sys_deri: @neuron_sys_deri
               sys_dtau: @(it,x,p,nx,np)df_derit(funcs,it,x,p,nx,np)
             sys_mfderi: [function_handle]
           x_vectorized: 0
                 tp_del: 0
      sys_deri_provided: 1
      sys_dtau_provided: 0
    sys_mfderi_provided: 0

Save and continue to continuation and stability of steady states demo1_stst.html

save('demo1_funcs_results.mat');